纵观近年来初中物理或科学课程,电学部分依然是学习的重点和难点,除了这部分内容知识系统性强,方法灵活外,更是训练题型多样的变换和科学探究活动真正训练学生的学习思维和学习方法。电学知识博大精深,变化无穷,在此仅就电学I—U图线的作图方法与其独特的应用提出几点思考和总结,希望能对大家的学习和研讨带来方便。
一,I—U 图线的作图与物理意义:
I—U 图线又叫伏安特性曲线。其物理意义主要有以下几个方面:
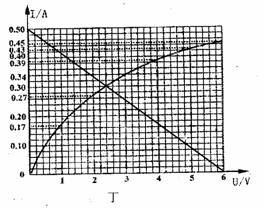
(1)它是指用图线来表示导体中的电流跟电压的关系 , 若横轴表示通过导体中的电流I, 纵轴表示导体两端电压U, 画出的I—U图线(如图1—2)就是导体的伏安特性曲线过原点且为直线的伏安特性曲线 , 表示导体两端的电压与通过导体的电流成正比 , 比值U / I即为导体的电阻 R .
(2)通常的I—U图线有如下两种,如图1—1和1—2,那么图1—1表示的意义可以通过上面的提示得到:当I 和U 的位置互换后,比值I / U表示导体电阻的倒数,即1/ R。
(3)图线为直线说明导体电阻为定值,当电压增大(或减小),电流也随之增大(或减小)。即对于欧姆定律的变形公式:R = U / I 我们不能说电阻跟电压成正比,跟电流成反比。
(4)有时我们会看到如图1—3和图1—4的曲线图,它们表示的又是什么意义呢 ?因以为它们的I—U图线不是直线,即电压和电流(或电流和电压)的比值不是定值,说明电阻R 在改变,初中范围内,大多数考虑的是温度对电阻的影响,即电阻会随温度的升高而增大。你能从图中曲线的弯曲方向判断电阻的变化情况吗?如果电阻值随温度升高而减小,那么图1—3和图1—4的曲线又该怎样画呢?
总之,如何正确理解伏安特性曲线的意义是巧妙运用I—U 图线的关键。
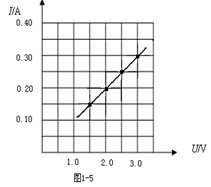
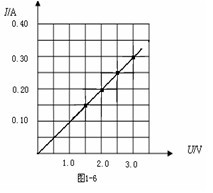
【例 1】以下表格是某同学在“伏安法测电阻”实验中测得的电压,电流值。请在下面坐标图中绘出电流与电压的关系。
|
电压(V) |
1.5 |
2.0 |
2.5 |
3.0 |
|
电流(A) |
0.15 |
0.20 |
0.25 |
0.30 |
【解 析】
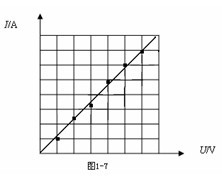
所以,作图时注意两个很重要的原则:
(1)伏安特性曲线过原点;
(2)不考虑温度影响时,伏安特性曲线为直线,为了减小误差,要让所描的点(包括原点)均匀分布在直线的两侧,而千万不要连成折线(如图1—7)。
二,I—U 图线的应用:
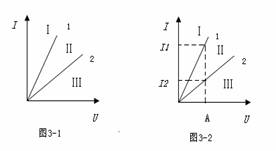
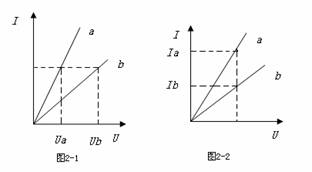
如右图I—U 图线表示a,b两导体的电阻,要比较其电阻大小有两种方法:
其一,如图2—1,作出相同电流 I 对应的电压分别为Ua, Ub,根据图线知:Ub >Ua。由电阻计算公式R = U / I 知:I 相等,Ub >Ua时,R b > Ra。
其二,如图2—2,作出相同电压U 对应的电流压分别为Ia, Ib,根据图线知:Ia > Ib。同样由电阻计算公式R = U / I 知:U 相等时,Ia > Ib,R b > Ra。
当坐标系中电压 U 与电流 I 位置互换后解决方法相同,在此不再赘述。
现在看此方法在实际例题中的应用:
A. R1>R2
B. R1 、 R2 串联后的总电阻的 I-U 图线在区域Ⅱ
C. R1 、 R2 并联后的总电阻的 I-U 图线在区域Ⅲ
D. R1 、 R2 并联后的总电阻的 I-U 图线在区域 I
【解 析】
为了更清楚地认识 I-U 图线 , 我们首先通过图线来比较一下两个电阻的大小 .
如图3-2所示 , 过横轴上任意一点 A 作平行于纵轴的直线交两图线于两点 , 设此两交点的纵坐标分别为 I1 和I2 .由图可知: I1 >I2.根据电阻的定义 R=U/I知: R1 < R2
当 R1、R2 串联后总电阻变大 , 故总电阻的 I-U 图线应在区域Ⅲ. 当 R1 、 R2 并联后 , 总电阻变小 , 故总电阻的 I-U 图线应在区域Ⅰ.正确答案 :D.
另一种方法请大家自己尝试,在此不再赘述。
应用二:根据图线求电压、电流或电阻:
能从I—U 图线中读出其中的信息,并灵活运用在实际解题中往往会起到事半功倍的作用,我们看以下例题:
【解 析】
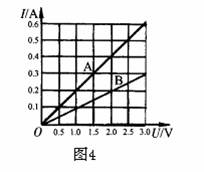
我们可以从两种不同的解法来对比I—U 图线带给我们的方便:
方法一:常规办法:对A图线,读图知I—U 图线为直线,电阻不变,从直线上任意一点(除原点外)的电压和对应的电流都可以求电阻,那么我们选最后一个点。
当U =3.0V,对应的 I=
同理得RB = 10 Ω。
A和B并联,总电阻 R = RA· RB /(RA + RB)= 10/3 Ω
总电流 I = U / R = 2.5V/(10/3 Ω)=
方法二:同上:当U =3.0V,对应的 I=
当A和B并联时,电压相等,UA = UB = U’ = 2.5 V
通过读图,A和B在电压为2.5V 时电流:
IA =
总电流 I = IA +IB =
通过对比两种方法,我们不难发现用方法二更简便快捷,充分体现了图解法的优势。
另外,此题可以进行延伸:如第二空可以作如下改变:将A和B串联后接在电流为
此题依然可以用图解法来解决:A和B串联后,U = UA + UB = 1.5V + 3.0V =4.5V。
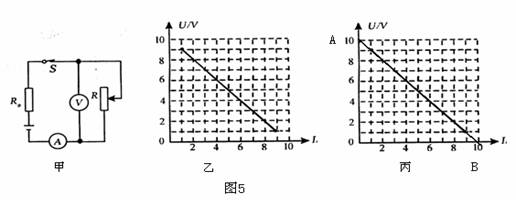
【例 4】如图5(甲)所示电路中,R为滑动变阻器,R0为定值电阻,电源两端的电压不变,改变R的滑片位置,电压表示数随电流变化的图线画在图5(乙)的坐标系中,则根据以上条件可知R0的阻值为_______Ω,电源电压_______V。
【解 析】
如图5(甲)所示电路中,R与R0串联,电压表测R两端电压U,电源电压U0 = U R+ U
= I ·R0 + U ,且电源电压U0保持不变,即U = U0 - I ·R0,故 I-U 图线为倾斜向下的直线。
作图:将直线两端延长分别与两坐标轴相交于A(
则对A点:当I =0,可认为是滑动变阻器某处断路,定值电阻R0和电流表相当于导线,此时电压表测得的即为电源电压,读图知A点,U0 = U = 10V;
对B点:当U = 0时,即滑动变阻器滑片在最下端,R = 0,电路只有R0 ,则R0 = U0 / I=10V /
其实此方法将来我们在高中要进一步学习的,实际就是“测电源电压和内阻”。通过对图象进行处理(延长),并求得交点坐标和充分利用交点的物理意义才是解决实际问题的关键!
应用三:作图法巧妙解决实际问题:
我们还是从作图法在解决中考题中的巧妙应用来看其巧妙的作用。
【例 5】如图6-1所示为白炽灯L1 (220V,100W)、L2(220V,60W)的伏安特性曲线,则根据该曲线可确定将L1、L2两灯串联在220V的电源上时灯的实际功率之比大约为( ) A.1:2 B.3:
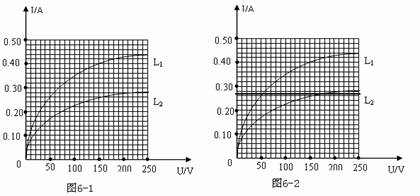
误解:一看题目我们马上就联想到告诉额定电压和额定功率用公式:R = U2 / P求电阻,然后两电灯泡串联电流相等,根据P =I2 R可得功率之比为电阻之比,而RA=2202/100Ω,RB=2202/60Ω,所以功率之比为:PA:PB =3:5,
图象似乎完全没起到作用,其实只要我们仔细想想就知道错误的原因:电灯的电阻是随着温度的升高而生高,当灯泡正常发光时,灯泡的散热与灯丝的生热达到平衡,灯泡温度不变,其电阻也就不再改变。也就是说,由额定值计算出的电阻是灯泡正常工作时的电阻。灯泡不正常工作时的电阻是无法计算的。所以RA =2202/100Ω,RB =2202/60Ω是没有依据的,因此功率之比3:5是错的。
【解 析】
作一条平行横轴的直线,与两条曲线有两个交点,过两个交点分别做两条竖直线交横轴与两个电压值,并使两个电压值之和为220V(如图6-2),这条水平横线的值就表示流过两串联灯泡的电流,大约得灯泡电压UA =55V,U B =165V, 根据P = IU可求得功率之比为1:3。
可见,熟练掌握图象处理可以化繁为简。我们再看一题:
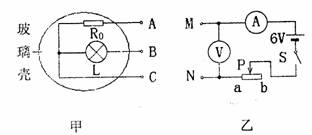
【例 6】(2006宁波市(课改区))某科学兴趣小组的同学在实验室发现一个有趣的元件(如图7,甲所示):透明玻璃壳内有一个标有"6V 3W”字样的小灯泡L(阻值不变)和一个由一种特殊金属丝制成的导体R0,A,B,C是其外露的三个接线柱。为进一步了解导体R0的某些特征,他们使用了如图乙所示电源电压恒为6伏的实验装置:把导线M,N分别与A,C接线柱相连,闭合开关S,移动滑动变阻器的滑片P,测得了一组电流表和电压表的读数,并绘制成图丙所示曲线。
(1) 小灯泡L的电阻值为_欧姆,当它正常工作时,通过的电流是 安培。
(2) 小明同学在原来连线的基础上,再用导线连接A、B两个接线柱,闭合开关S,把滑片P移到a端,此时电流表的示数是多少安培?
(3)若把导线M、N分别接到A、B接线柱上,闭合开关S,把滑片P移到a端,则小灯泡消耗的电功率为多少?(温馨提示:本小题可用作图法辅助求解)
【解 析】
(1) 小灯泡"6V 3W”分别表示额定电压和额定功率,
R = U2 / P = (6V)2/3W =12Ω ;
正常工作时,I = U / R = 3W /6V =
(2) 当M,N分别与A,C接线柱相连后再用导线连接A、B两个接线柱, R0与灯泡L并联,且P移到a端时,U = 6V
读图知R0电流I0 =
灯泡正常工作时, I L =
电流表的示数 I = I0 + I L =
(3) 若把导线M、N分别接到A、B接线柱上,
R0与灯泡L串联,总电压U = 6V = U Lˊ+ U0 ˊ
即:6V =12Ω· I0ˊ + U0 ˊ
作出I0ˊ与U0 ˊ的关系图线(如丁图),与原线相交得到: I0ˊ=
则小灯泡消耗的电功率P Lˊ = U Lˊ· I Lˊ= (U ﹣U0 ˊ) ·I Lˊ=( 6V ﹣2.4V) ·
问题解决完了,我们可以再思考一下:此题不用作图法就无从下手了。因为此题中导体R0的I—U 图线特征是曲线,线上任何一点都满足其特征,或者说曲线表示了它在测定范围内电压与电流的所有特征,但只有一条曲线我们就无能为力了。所以只有我们得到了I0ˊ与U0 ˊ的另外一个关系图线,其交点就是它同时满足的电流与电压条件,作图求出此时的电流和电压,这也是我们解决此题的关键点。
在此简单地总结了I—U图线在实际作图中的注意事项和解决实际问题中的几种方法,而其应用在解决科学问题时将是不胜枚举的。并且,与此类似的图线在表示两个物理量(如质量与体积,匀速直线运动中的路程与时间等等)的关系时经常会碰到,其解决方法完全是类似的,我们只有充分理解其意义,熟练掌握其方法,解决实际问题时我们才能出奇制胜,游刃有余。
- 上一篇资讯: 提高课堂合作学习有效性策略研究
- 下一篇资讯: 装置气密性检查的几种方法