一、教学目的：

1)  能通过对不等式应用题的理解，建立数学模型；

2)         掌握利用不等式求最值的方法；

3)         培养学生主动探究，自觉学习的精神；

激发学生创新意识，开发学生的创新潜能。

二、教学重点：建立数学模型解决实际问题

三、教学难点：利用不等式求函数最值

四、教学方法：启发探究式

五、教学手段：多媒体电教辅助

六、教学过程：

（一）  创设情景，提出问题：

教师设计了一段看似与数学无关，但令学生十分感兴趣的话进行引入——

引言： “近十几年，我们的祖国在各个领域取得了瞩目的成就，成为国际上一个举足轻重的国家，令人骄傲。特别是近期召开的“十六大”上提出的“全面建设小康社会”的国策更令人鼓舞。

我们湖大附中继成为市示范高中之后，又向着省示范高中的目标迈进！美化校园、

建设校园的规划工作也进入了一个新的阶段！

李玉新校长说，希望用最少的钱办成最好的事。今天就让我们一起，利用大家的智

慧，运用数学知识来帮助校长实现这个愿望。”

这番话成功的把学生的情绪和主人翁意识调动起来，于是教师“趁热”将问题抛出

—— 征集“花房工程”的设计方案。

1）利用课件展示“花房工程”：

校园西侧有一面旧墙长14米，现准备利用这面旧墙修建一个平面图形为矩形，面积为126米 的花房。工程条件是：① 修1米旧墙的费用为 元；② 拆去1米旧墙所得的材料修建1米新墙的费用为 元；③ 建1米新墙的费用为a元。

2)    请学生积极思考，作为设计师,设计建造花房的不同设计方案。启发学生通过

相互讨论，对各种设计方案进行理解、比较。这个问题设计的起点低，使每个学生都可以动手，营造一个“人人参与”的局面，给每个学生提供体味成功的机会。

(二) 深刻理解，大胆尝试：

鼓励学生根据开放题的叙述，结合自己的设计，口述各种方案施工简图的画法。教师通过课件直观展示绘制简图的过程。通过比较，认识各种方案的不同之处。通过归纳，方案大致为两种：

（方案一）利用旧墙的x米（x<14），作为矩形花房的一面边长；（方案二）矩形花房的一面边长为x米（x 14）.

 

14米

x 米

126米2

（方案一）

 

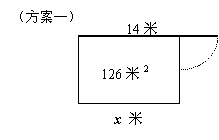
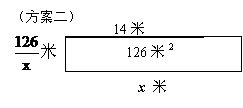
这两种方案的区别是：第一种方案有拆旧建新的施工环节，而第二种方案则没有。

其中的x表示利用旧墙修建的矩形的一边边长，在方案（一）中，0<x<14；而在方案二中，x≥14。同学们还会设计看似不同于上面两种的其他方案，但从施工方式的角度来看，则皆可归于其中一种。这个课件展示过程的目的在于：

（一）直观校对学生绘制简图的正误；

（二）隐性地启发学生对简图中每个量的思考，为后面问题的进一步处理打下基础。

(三) 探索研究，得出结论:

将设计不同方案的同学分为几个小组，让他们计算自己设计的设计方案的最低造价。经过同组成员的共同思考、协作、互评，最终选派一名同学上台向大家展示成果。第一种方案将总造价y表示为关于x(0<x<14)的函数,利用均值不等式求解: 当x=12米时，最低造价为35a元。第二种方案同样将工程总造价y表示为关于x(x≥14)的函数,学生容易同样利用均值不等式求解，而实际上取最值时等号成立的条件不成立。应利用函数的单调性来解决这个求最值的问题，当x=14米时，最低造价为35.5a元。对这个学生易错的环节绝不能给予事先预防，应让学生充分暴露其思维过程，获得结论。再引导学生对自己得到的结论进行全方位的评析，自行修改完善，主动纠错。这样，既可提高学习效果，又能优化思维品质，有助于对知识的理解与深化，自觉形成新旧知识的结构体系。这就是所谓的“借误导悟”。

对“成果”的评价采取自评和互评的方式，选出大家心中的“最佳”方案。让学生畅所欲言，从造价，施工方式，工期，以及利用土地状况等诸多因素进行考虑、评价。最后，教师分别从“最实用性”、“最少预算”、“最佳创意”等多个角度对每个设计方案进行肯定。充分珍视和保护每个学生的每一个思维火花，每一次学习激情。

(四) 反思感悟，小结要点：

1）   解不等式应用问题的步骤：

阅读理解材料

建立数学模型

讨论不等关系

做出问题结论

2）   利用均值不等式应注意的问题：“一正二定三相等”；

3）   在使用均值不等式求最值时，若等号不能取得，须考虑利用函数的单调性求解。

(五) 学以致用，开发潜能：

趁学生意犹未尽之际，拿出校园规划问题之二 ——

草坪小径问题

请问怎样修能使这条小路的长度最短，用料最省？

将这个开放性问题留作课堂之外的探究，开放探索空间，提供更自由的数学活动。    

最后，送给学生一段寄语：“今天，我们在一起研究并解决了一个身边看似复杂，却在我们能力范围之内的开放性问题。希望大家今后能够学习用理性的思考、丰富的知识，去面对、去认识、去分析、去解决学习生活中的一切问题！”良好的数学品质不仅仅只包括数学知识。

七、课后记：

通过对这节开放式授课的设计分析，我们不难了解开放式课堂教学要求教师更新思想，更新教学态度，更新教学方法。我们不难看到开放式课堂教学活动，不仅使能力较强的学生能参加更多的活动，同时也使能力较低的学生能根据自己的能力和兴趣踊跃参与体验数学活动。师生之间、学生之间的多向交流有利于消除传统授课过于拘谨的场面；有利于缩短师生距离；有利于学生积极思索，勇于发现，敢于提出问题；有利于学生探究意识和创新精神的培养和发挥！给学生一个机会，他们定会还你许多惊喜！